The P4 programming language is the interface of choice for programmable data plane devices. P4 programs have to meet network throughput requirements, but they are also subject to resource constraints imposed by the hardware. Compilers and human programmers try to optimize code to meet these constraints, which is hard enough as it is—but how can you be sure all those complex optimizations don't introduce new bugs? In other words, how might you check that your optimized program is equivalent to the original, better-understood version?
This is known as program equivalence, and in compiler research a tool for checking equivalence after optimizing or compiling a program is known as a translation validator. There is a long history of building tools like this for general purpose programming languages and even for P4, but we found that P4 parsers in particular are an interesting new domain in need of a good equivalence checker.
Our new tool Leapfrog is just that, an equivalence checker for P4 parsers. Moreover, Leapfrog produces proofs which can be independently checked by the Coq general purpose proof checker. This is useful for Coq programmers, who do all kinds of work inside the theorem prover that can build on Leapfrog results, but it is also encouraging because it means the equivalence checking algorithm's results are ultimately guaranteed by an independent verifier. You do not have to understand the inner workings of Leapfrog to trust its results–but it can't hurt.
Read on to see Leapfrog in action and learn a little about the theory that makes it work. For all the details, written for an audience with some fluency in programming language theory, see the paper. The conference talk is also available on YouTube.
Example
Below, in graphical form, are two parsers for UDP encapsulated by MPLS. They parse MPLS headers until they see one with its bottom-of-stack marker (the 24th bit) set, and then they parse UDP and accept the packet. The first parser solves this 2-header parsing problem with a 2-state automaton. The second parser is more complex: it has been optimized to speculatively parse two MPLS headers at a time, which improves throughput on some P4 compilation targets by consuming more of the packet in each parsing step. We call this optimization vectorization, by analogy with the classical compiler optimization of the same name.
Getting vectorization right requires some care, because if the first MPLS header is the bottom of the stack, the second MPLS header will in fact be half of the UDP header. The state q5 addresses this edge case by parsing the remaining chunk of the UDP header out of the packet and concatenating it onto the mistakenly parsed MPLS data.
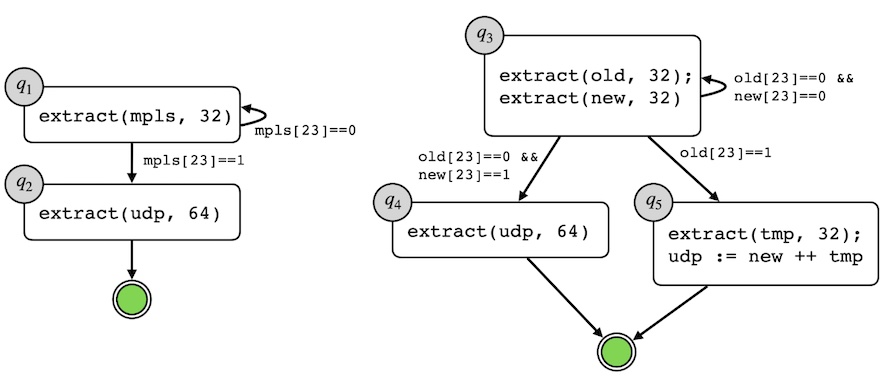
Simple parser (left) and optimized parser (right). Parsers begin from their topmost state (q1 at left, q3 at right). The doubly-outlined green circles are the accepting states for the automata.
In Leapfrog, these parsers are encoded into P4 Automata (P4A), a domain-specific language that captures the essence of the P4 parsing sublanguage. Here is the Coq code that corresponds to state q1 above.
{| st_op :=
extract(HdrMPLS) ;
st_trans := transition select (| (@EHdr header sz HdrMPLS)[23 -- 23] |) {{
[| exact #b|1 |] ==> inl ParseUDP ;;;
[| exact #b|0 |] ==> inl ParseMPLS ;;;
reject
}}
|}
Actually proving that the two automata are equivalent is straightforward. The notion of equivalence we are interested in is called language equivalence. The language associated with an automaton is the set of strings of bits that it accepts, and two parsers are language equivalent when their languages are the same. We begin by stating equivalence to Coq as a theorem, using the lang_equiv_state predicate from Leapfrog's P4A semantics. The first two arguments are the automata and the second two arguments are the initial states which we assert to be equivalent.
Lemma mpls_equiv:
lang_equiv_state
(P4A.interp Plain.aut)
(P4A.interp Unrolled.aut)
Plain.ParseMPLS
Unrolled.ParseMPLS.
Next, we invoke Leapfrog's equivalence checker tactic with a couple of helper functions for checking equality between states and a flag to enable/disable an optimization called hash-consing. We disable the optimization here because it is only beneficial for larger benchmarks.
Proof.
solve_lang_equiv_state_axiom
Plain.state_eqdec
Unrolled.state_eqdec
false.
Qed.
This completes the proof. The equivalence algorithm is symbolic, meaning it uses logical formulae to represent portions of the joint state space of the two automata. Operations on this symbolic representation require checking the satisfiability of entailments between formulae, something Coq cannot do automatically. Leapfrog uses an SMT solver in the loop to decide these satisfiability problems.
P4 Automata
Before we can explain how Leapfrog works and what we've used it for, we should first describe the programs Leapfrog can analyze. Leapfrog does not work on a standard programming language or intermediate representation like P4, C, or LLVM IR. Instead, Leapfrog defines its own language of P4 automata which is meant to capture most uses of the P4 parser language while avoiding its more esoteric features.
Abstractly, a P4 automaton (P4A) has five parts:
- St, the set of stores, usually finite maps from header names to values.
- S, the set of state names.
- sz: S → int, the size function. (sz s) is the number of bits extracted in each state and must be a strictly positive number.
- update: S → list bool → St → St, the update function. It describes how the automaton updates the store in a state s, given a list of bits of length (sz s).
- transitions: S → St → S + {accept, reject}, the transition function. After running a state, this function is used to select the next state to run, or indicate rejection/acceptance.
All this comes together in the semantics, which define a step relation (s, st, buf) →b (s', st', buf'). The buffers buf and buf' are lists of bools (bits), and the subscript indicates the bit currently being read. The states s and s' are drawn from the extended state space (S + {accept, reject}), whose inhabitants have the form (inl s), (inr accept) or (inr reject).
There are three kinds of step.
- ering: if len(buf) + 1 < sz st, then (inl s, st, buf) →b (inl s, st, buf ++ [b]).
- Transitioning: if len(buf) + 1 = sz st, then (inl s, st, buf) →b (s', st', []), where st' = update(s, buf ++ [b], st) and s' = transitions(s, st').
- Termination: (inr x, st, buf) →b (inr reject, st, buf).
Observe that buffering steps never change the state or store. This makes them pretty boring from a verification perspective, and one of the tricks in Leapfrog has been to coalesce strings of buffering steps into "leaps" over chunks of the input packet. But doing this right is a little subtle, so we'll return to it in the Optimizations section below.
A state s accepts a word (bitstring) w = b1 b2 … bn if there is a string of transitions s →b1 s' →b2 …→bn accept. The language of a parser, given a distinguished start state start, is then the set of strings accepted by start. This is a familiar concept from automata theory, being the language of the finite automaton defined by the step relation →b.
Then language equivalence of P4A is equality of their languages as sets of strings.
Bisimulation
Bisimilarity is a central concept in coalgebra, the study of automata-like mathematical objects, with its origins in the academic field of process algebra. Two automata are bisimilar if a bisimulation exists between them. A bisimulation between a1 and a2 is a binary relation R on their respective state spaces S1 and S2 such that
- (start1, start2) is in R.
- If (s1, s2) is in R and b is a bit, then (step s1 b, step s2 b) is in R as well.
- If (s1, s2) is in R then s1 is accept if and only if s2 is accept.
Bisimilarity implies language equivalence, and vice versa, so it is possible to decide language equivalence by giving an algorithm for deciding bisimilarity. The usual way to do that is to compute some kind of candidate bisimulation by searching the joint state space of the automata. Here is a naive decision procedure for bisimilarity in that style.
R := {}
T := {(start1, start2)}
while T nonempty:
pop (c1, c2) from T
if (c1, c2) is in R
then continue
else add (c1, c2) to R
add (step(c1, true), step(c2, true)) to T
add (step(c1, false), step(c2, false)) to T
return (forall (c1 c2) in R, accepting(c1) <-> accepting (c2))
This is as simple as bisimulation algorithms come, but it is also inefficient for realistic P4 parsers. For instance, an IPv6 header is 40 bytes = 320 bits long. This means the algorithm will have to fit 2^320 intermediate states into the relation! A direct search of such an enormous state space is beyond impractical, and our implementation of this algorithm failed to finish on all but the most trivial programs from the benchmark suite.
Optimizations
The Leapfrog algorithm makes this search tractable using a few optimizations: symbolic bisimulation, bisimulation by leaps, and reachability analysis. There is more going on than just that. For instance, we perform a backward search rather than a forward one as presented here. For all the details, see the paper.
Symbolic Bisimulation
Rather than represent R by a concrete set of configurations, we use a symbolic representation. This lets us represent sets of large cardinality in a compact symbolic form. You might compare this to state-space reduction techniques in model checking, which reduce a potentially complex exhaustive testing problem to a more tractable symbolic search.
Fix a logic L with formulas φ denoting binary relations on configurations. To represent R and T above, we use a list of formulas [φ1; φ2, …, φn]. The list is interpreted as a big disjunction φ1 ∨ φ2 ∨ … ∨ φn. Then we can rewrite the algorithm to work over formulas, assuming we have a symbolic evaluation operator step_sym(φ, b).
R := []
T := [φi] // where [[φi]] = {(start1, start2)}
while T nonempty:
pop φ from T
if φ⇒R
then continue
else add φ to R
add ∀b:bit.step_sym(φ, b) to T
return R⇒φa
where [[φi]](c1, c2) = c1 == start1 and c2 == start2
and [[φa]](c1, c2) = accepting(c1) ⇔ accepting(c2)
Implementing this algorithm requires a logic L that is sufficiently expressive to implement a symbolic evaluator as well as decision procedures for checking the validity of entailments φ⇒R and R⇒φ.
Bisimulation By Leaps
While taking one symbolic step in each iteration of the algorithm is an improvement over taking two concrete steps, it is still needlessly expensive. As alluded to earlier, most single bit transitions taken by a P4 automaton only put bits into the buffer and do not change the state or modify the store. These buffering transitions can be batched into a single invocation of the symbolic evaluator in what we call bisimulation by leaps.
Doing this properly requires saying a little about the form of the assertions φ which so far has been left unspecified. Rather than being unconstrained, they must begin by asserting the current automaton state and buffer length for each automaton being analyzed, like this:
<state1, len1> <state2, len2> ⇒ φ'
The formula φ' only talks about the contents of the buffer and store. The two templates in angle brackets constrain the state and buffer size.
Given a pair of templates, we can determine the largest leap that the algorithm may take. Recall each state in a P4A extracts a fixed number sz(s) of bits. The leap size is then min(sz(state2) - len2, sz(state1) - len1). There is some special behavior for accept/reject states which I am eliding here.
Then the full algorithm is as follows.
R := []
T := [φi] // where [[φi]] = {(start1, start2)}
while T nonempty:
pop φ from T
if φ⇒R
then continue
else add φ to R
add ∀b:leap_size(φ).leap_sym(φ, b) to T
return R⇒φa
Reachability Analysis
In fact, the algorithm we use is a backward analysis built around a weakest precondition predicate transformer instead of a forward symbolic evaluator. In this context, it is important to also bound the states the WP operator tries to explore, since it might take a while for a backwards search to determine that a configuration is unreachable.
To address this performance problem we run a reachability analysis before beginning the main algorithm. This produces a list of possibly reachable templates which the algorithm uses to prune unreachable states early, avoiding a lot of pointless work and reducing the size of the intermediate symbolic relations.
Benchmarks
We validated Leapfrog against a suite of benchmarks, ranging from simple and somewhat contrived test cases to more realistic and complex applications. A full accounting of the different benchmarks is available in section 7 ("Evaluation") of the paper. Here I will just go through a couple.
First, there is the speculative loop example from the start of this blog post. Leapfrog verified that the two parsers shown in the example are the same in about 4 minutes. While this is a reasonable time scale, for such a simple example this kind of performance is disappointing, and we are hoping to optimize Leapfrog further in future work.
Second, we used Leapfrog to perform translation validation. It is quite common for compiler optimizations to have ill-behaved edge cases and bugs which can cause miscompilations, in which the observable behavior of a compiled program fails to match the intended behavior of its source program. A translation validator can check that a particular run of the compiler was safe by comparing the behavior of the source and compiled programs for equivalence (or, as is usually the case, refinement). We took the parser-gen compiler, which compiles a P4A-like source language to a low-level set of table rules, mostly automatically lifted the table rules back into P4A, and compared them with Leapfrog to validate compilations. See Figure 8 from the paper below.
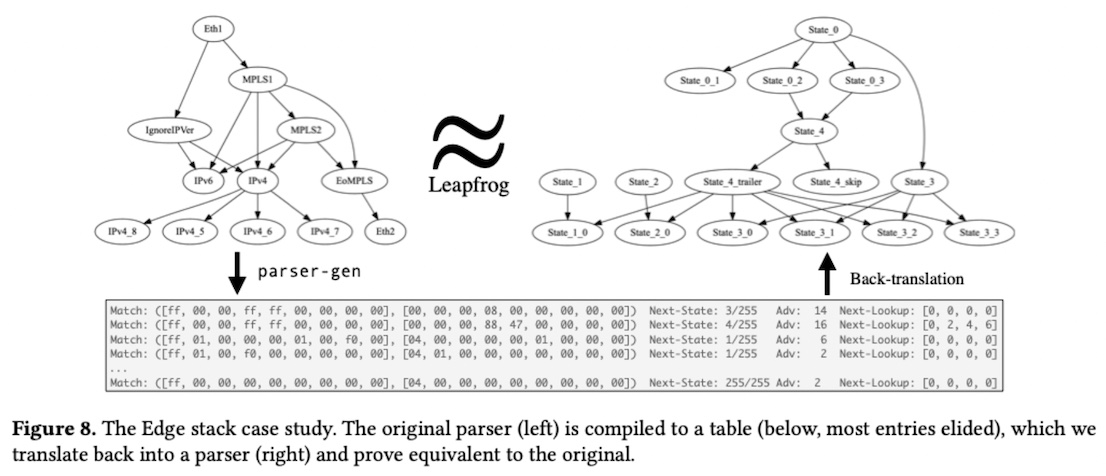
While we have not yet scaled Leapfrog and our back-translation tool to deal with more complex examples, this was a promising initial result.
MirrorSolve
There are a number of tools for incorporating SAT/SMT solving into deductive theorem proving. We found that the existing options did not quite match our use case and ended up writing a new tool called MirrorSolve.
MirrorSolve is a Coq plugin and tactic that can dispatch goals written in its first-order syntax. This means a development using MirrorSolve gets precise control over the SMT query it is making, rather than relying on a translation from Coq formulas to first-order logic that may introduce complications or fail to handle certain kinds of Coq propositions.
For flexibility, MirrorSolve produces queries in the interoperable SMT-LIB format and can be configured to use different solver backends. For Leapfrog we use CVC4 and Z3, depending on the benchmark. Certain queries seem to cause problems for Z3 but work in CVC4, and vice versa.
While it looks possible, for now MirrorSolve does not use the response of the solver to construct a proof object. Instead the TCB of MirrorSolve includes its Coq plugin which prints and reads SMT-LIB syntax as well as the solver used to dispatch the query. Proof reconstruction could completely remove these components from the TCB.
Conclusion
In this blog post we introduced Leapfrog, a verified equivalence checker for P4 parsers. By exploiting classical techniques from automata theory, Leapfrog is able to prove parser equivalence fully automatically. The results are verified in Coq against an independently auditable semantics of P4 parsing.
For more details, see the paper on arXiv. Leapfrog is available on Github, as is the Mirrorsolve plugin. Please let us know what you think, and we're happy to answer any questions you may have.

